
 |
|
|
 |
|
|
 |
| Мысли вслух...Возможно есть и ошибки... |
|
Постов: 8
Дата регистрации: 16.02.2008 |
Цитата, автор butaev:
я не понял вот эту строчку в Вашем посте: "при n=200, а=2% получился график средний между а=1%n=100 и а=1%n=400". Не поясните ли. Непонял про разные "а" и средний.
|
Еще до поста Юрия "Добил эту темку Уфф"
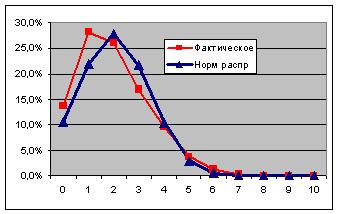
Я проводил эксперимент в Excel - сделал 250 выборок с параметрами n=200, а=2%.
Эксперимент повторил 10 раз - графики были похожи, но чуть различались, поэтому усреднил результаты по 10*250 выборок
получилась картина (см. ниже).
|
|
 | | Пример2.JPG |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   16.02.2008 08:14 16.02.2008 08:14 |  |
|
|
|
Постов: 8
Дата регистрации: 16.02.2008 |
На мой взгляд картинка как раз промежуточный вариант между двумя графиками на рис. Ошибка 3 у Юрия.
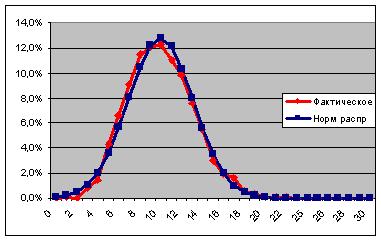
Затем, я задал параметры n=200 и a=10% и по той же технологии получил уже почти нормальное распределение(см. ниже).
Таким образом, доля в 10% компенсировала маленький размер выборки(Пример3) а при уменьшении доли (см. выше Пример 2) имеем распределение, отклоняющеся от случайного. Насколько хорошо это учитывает распределение Стьюдента? Если я помню, там 1,96 конечно действует для n=бесконечности,
но на практике берется уже при выборке >120.
|
|
 | | Пример3.JPG |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   16.02.2008 08:20 16.02.2008 08:20 |  |
|
|
|
Постов: 2758
Дата регистрации: 31.08.2005 |
для: IgorRudy© Игорь, во-первых, мы обсуждаем, по сути, распределение биномального признака, откуда там будет "второй горб"?
Во-вторых, даже если рассматривать некоторый признак, как распределенный отлично от нормального распределения (например, получение AIR как "среднего нормального распределения аудиторий номеров за определенный период" является ошибочным, аудитории конкретных номеров имеют не-нормальное распределение), то тогда требования к объему выборки СНИЗЯТСЯ!!! Для Уилкоксона 22 наблюдения, при использовании Манна-Уитни вообще достаточно 20 (при больших значениях пользуются нормальной аппроксимацией).
Господа, мы вообще что собираемся измерять? Какую выраженность признака? И что потом с этим знанием делать?
Не забывайте, что признак имеет собственную динамику даже во время его измерения, тем более глубоко ошибочным является предположение, что он останется неизменным сколько-нибудь длительное время. Целью всех медиаисследований является получение относительных размеров аудиторий носителей относительно друг друга, для расчета удельной стоимости, и если ошибки несистематические, то их величину можно игнорировать.
И еще, какая разница, с какой точностью измерен признак, если он маленький, до нескольких процентов? В практическом плане это НОЛЬ, так как слабые признаки неусточивы в социальных системах по определению. Я понимаю, что кого-то могут интересовать именно люди, которые обладают именно этим признаком, но чаще всего он является вторичным, т.е. надо не сравнивать аудитории каки-то специальных изданий по результатов репрезентативных опросов в несколько тысяч человек, а опросить две-четыре сотни людей, обладающих первичным признаком и выяснить, что же именно они читают. Или вообще забить на эти носители и заниматься директ-маркетингом по той, пусть и в десятки тысяч людей, группе, которая интересует. Любые затраты в специализированные издания в России являются рискованными в той части, которая приходиться на розничную часть тиража. ЛЮБЫЕ!!! Тогда и сравнивайте удельную стоимость по числу подписчиков, оно же известно с 100% точностью (минус потери в почте  ). ).
Вообще я как-то устал наблюдать желание b2b работать по законам потребительского рынка и надеяться на эффекты отклика по закону больших чисел. На этом рынке каждая сделка уникальна и отношения личные, что мы хотим увидеть полезного для принятия решений в результатах населенческих репрезентативных опросов? ЧТО? А какая разница, какая же именно аудитория носителя, если она меньше 5% по целевой группе на массовом рынке? Нам это должно быть безразлично, так как этот носитель на массовом рынке нам не нужен, если только вас не интересует аудитория именно этого носителя (хотя задача странная, так как любая целевая -демографическая, доходная, профессиональная- группа в разы, а то и в десятки раз, больше аудитории любого носителя).
Также, господа, напомню, что то, что мы в своих дискуссиях называем "ошибкой выборки" таковым не является, мы под этим обзываем "доверительный интверал" с той или иной заданной точностью. Ошибка выборки для признака в 1% становится меньше замеренной величины (0,995%) уже при выборке в 100 наблюдений, а уж какой доверительный интервал выбрать это все уже дело вкуса. И вообще, что менятся с точки зрения решения, если при выборке в 200 человек у нас признак в 1% имеет доверительный интервал 0-1,7% или 0-2,4% или 50% 46,5%-53,5% или 43%-57%. Если у вас правильно построена выборка, вы же знаете, что при увеличении выборки вы не выйдете за ошибку выборки (доверительный интервал при t=1, посмотрите результаты Developer, они же именно это демонстрируют: смещение вправо относительно нормального распределения малых величин ), и если даже при малой выборке у вас два объекта получили по 50%, а после многократного увеличения выборки вы узнаете, что на самом деле у одного аудитория 48%, а у другого 52%, что изменится с точки зрения решения? Вот что?
Практически все маркетинговые решения можно принимать после опроса 200 человек целевой группы. Если мы с помощью опросов пытаемся компенсировать недостаток всякой рыночной информации (доли рынка и т.д.), то и тут вся значимая информация будет получена при выборке в 400 человек, а при 800 вы вообще будете знать "все и для решений и для любознательности". Основная причина увеличения выборок это желание знать взаимосвязи вторичных признаков, но это желание сродни желанию спровоцироват слонов в зоопарке на спаривание не ради размножения слонов, "а чтобы позырить". Интересно, часто очень интересно, но в практическом смысле бессмыленно; маркетинговая коммуникация эффективна только в том случае, когда она прямолинейна, как контрольный выстрел. |
|
--------
http://www.dnp.ru |
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
    16.02.2008 13:20 16.02.2008 13:20 |  |
|
|
|
Постов: 2128
Дата регистрации: 07.04.2005 |
Пост без формул….. 
Эта тема изначальна затеяна мной, что бы обсудить 2 вопроса:
1. ОШИБКА: Можно ли использовать формулу ошибки (Гаусс) для малых долей признака (a<1%).
2. НЕ МОНОТОННОСТЬ: Влияет ли, не монотонность распределения признака на вычисление его доли
Мой Ответ:
- на первый вопрос: Да можно, если выборка достаточна большая.
- на второй вопрос: Нет не влияет.
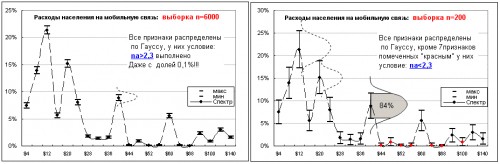
Надеюсь, что приводимые ниже графики помогут лучше понять поставленные в этой теме вопросы.
P.S. К точкам на графиках прошу не придираться, эти данные по сотовой связи я уже приводил здесь. Просто они были по рукой. Для иллюстрации можно взять любое другое распределение (медиапотребление, доход, и т.д….). В конце концов нарисовать от балды любую другою кривую, как я это сделал в 1 посте…..
|
|
 | | Спектр Мобилы.gif |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 01:59 17.02.2008 01:59 |  |
|
|
|
Постов: 8
Дата регистрации: 16.02.2008 |
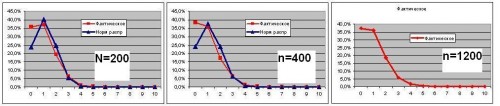
Ерунда получается - форма распределения зависит только от доли, но не от размера выбрки.
Я провел эксперименты для а=1% при n=200, n=400, n=1200 картинака примерно одинаковая - смещение к 0.
Таким образом, эксперимент показывает, что форма распределения не зависит от объема выборки, но зависит от доли (см. предыдущие посты):
чем доля ближе к 50%, тем форма распределения ближе к нормальной. На выборке в 200 форма стала нормальной при доле 20%. |
|
 | | а=1.JPG |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 09:28 17.02.2008 09:28 |  |
|
|
|
Гость<<
< |
Цитата, автор Юрий Рязанов:
1. ОШИБКА: Можно ли использовать формулу ошибки (Гаусс) для малых долей признака (a<1%).
- на первый вопрос: Да можно, если выборка достаточна большая.
|
При этом ошибка вычисляется "с большим запасом".
Если нет перекоса при формировании выборки, то малые доли НИКОГДА не будут расти при увеличении выборки n=1/p>2, в силу исторических причин можем постулировать, что в 2,3 раза. Собственно говоря, формула 13а как раз об этом (кстати, t-критерий 2,3 это 97% вероятность для больших выборок, для p=95% t меньше 2,3 с f=9)
для: Developer© а что Вас удивляет, вся теория статистики была построена на решении задачи, какую точность дает то или иное число подбрасываний с формально равновероятным исходом (да и то, в подбрасывании реальной монеты происходит апроксимация к 50%, а не колебание значений вокруг 50%) и в качестве базовой картинки вероятности используется "гауссовский колокол" и обычная формулировка "ошибка выборки в N человек составляет F%" под F% подразумевается ошибка 50% доли. Но это общая уверенность в типичности "нормального распределения" является последствием травм, полученных в системе образования. Посмотрите на график ошибки для доли в 1% и 50% в зависимости от выборки, по абсолютному значению точность замера малой величины выше, чем точность замера большой величины, этот момент как-то всеми игнорируется... А на самом деле, точность замера малой величины p равна точности измерения большой величины (1-p), то есть абсолютная относительная ошибка +- 1% для доли в 1% будет 100%, а для доли в 99% чуть больше 1%, но смысл - незначительность ошибки - от этого не меняется.
Соответственно, если вопрос Юрия Рязанова переформулировать в форме, а "какая выборка необходима для того, чтобы мы были уверенны, что доля признака в генеральной совокупности больше 99%" то 95% уверенность в этом у нас получается уже при 20 человек (при этом сам признак 100%), 98% при 100 (признак 99% или 100%) и больше 99% при 400 человек (при результате замера 99% и больше). Вообще, когда спорят о точности измерения малых величин как-то забывают, что в этой ситуации можно обсуждать точность величин (1-p) и тогда спор теряет смысл, так как относительная ошибка становится на порядок меньше. |
|
|
|
Постов: 8
Дата регистрации: 16.02.2008 |
Цитата, автор Гость:
Посмотрите на график ошибки для доли в 1% и 50% в зависимости от выборки |
Как вы расчитывали нижний ряд для 1%? Вероятно по M=корень(p*(1-p)/n)
Это расчет средней ошибки из предположения p=50 и нормального распределения, который я и как я понял Вы - отвергаем.
Вы предполагаете, что поскольку не по Гаусу, то расчет ошибки идет с запасом?
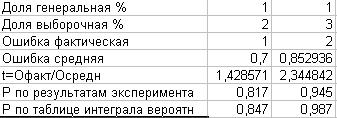
Посмотрите такую табличку. Допустим нам известно что в Генеральной совокупности доля p=1%.
Мы сделали 2 выборки n=400. В первой из них фактическая доля а=2%, во второй а=3%. Т.е. фактически ошиблись соответсвенно на 1% и на 2%.
Средняя ошибка при известных нам а по формуле М=корень(а*(1-а)/n) составит соотвественно 0,7 и 0,85
Чтобы дотянуть до фактической ошибки, возьмем соответсвенно t.
Далее по таблице интеграла вероятностей я определил вероятность того, что эта ошибка действительно предельная.
В предпоследней строчке сопоставил с вероятностью выпадения ошибочных значений в эксперименте для n=400.
Как видите с одной стороны различия небольшие но важно то, что фактическая вероятность выпадения неправильных значений будет выше табличной, значит, если использовать М=корень(а*(1-а)/n), и соответсвующий t, то мы приуменьшим погрешность.
Причем в последнем столбце разница между 95% и 99%.
|
|
 | | Расчет ошибки.JPG |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 12:39 17.02.2008 12:39 |  |
|
|
|
Гость<<
< |
для: Developer© Ваша таблица только демонстрирует значимость правильного формирования выборки. Практическая проблема в том, что корректность формирования выборки оказывается важнее всяких там табличных значений. В наших задачах, когда нужно не шары из ящика выбирать, а формировать выборку из людей, ошибки формирования оказывают гораздо большее влияние на получаемые результаты, чем смещения, даваемые выборочным методом как таковым. Что такое 12 человек в выборке с признаком, который должен был быть выявлен только у 4? Плохая организация полевых работ, "поиск под фонарем, а не там, где потеряли".
Вот тот же лентяй Стьюдент, ну доказал он, что доля выявляемого пойла из партий пива существенно не меняется при выборочном методе по сравнению с плошным обследованием. Разница в том, что потребителю не важна ошибка в выявлении пойла, он заинтересован в абсолютном исключении пойла из поставок в магазины и бары.
В наших же задачах мы часто не знаем истинного значения изучаемого признака, из-за этого можем доверять получаемым значениям только исходя из репрезентативности известных параметров: пол, возраст, образование, распределение по уровню доходов и т.д. А тут получается интересная штука, что, если исключить ситуации подлога интервьеров по регистрации этих базовых параметров, то при квотных выборках в 60 человек и при репрезентативных по городу в 400 человек все необходимые параметры стабилизируются (на национальных выборках с 1200). Соответственно, и получаемые результаты по малым величинам тоже (том в смысле, что при увеличении выборки они будут только потихоньку снижатся, но НИКОГДА не будут выше полученных значений на этих выборках).
Нас же что волнует в вопросе выборочных исследований: сколько людей мы должны опросить, чтобы выявить все разнообразие признаков, и сколько, чтобы не ошибаться в их выраженности. Ответ на эти вопросы очень сильно зависит от того, что значит "разнообразие": признак, встречающийся у отдельных экземпляров нас интересует? А три ореха это куча? ТО есть это вопросы уже не самой статистики, а совсем другого. В принципе, общая склонность к использованию 95% вероятности позволяет предположить, что исследовательское сообщество склонно игнорировать признаки, которые имеют выраженность менее 5%. На самом деле, сто лет назад так оно и было; сейчас же готовы рассматривать любые малые группы и вообще маркетинговая мода декларирует склонность к атропологическим исследованиям, а в них как раз уникальность важнее "общности".
Что же касается ошибки в определении выраженности признака, то тут очень важным является для чего мы что-то измеряем. Маркетологи склонны игнорировать, что управленческие решения по своей природе статистически очень грубы, или "да" или "нет", нельзя быть "немножко беременным". Соответственно, они ориентированны не на точные значения, а на пороговые (ниже определенного - не работаем, выше определенного - работаем), причем субъективно интерпретируемые. И уж точно, не на сравнении 0,6% и 0,72%, пусть они и получены на выборке хоть в десятки тысяч человек, так как это другие параметры, формирующие эти значения, куда важнее и куда грубее по своей природе, чем что стандартная ошибка или доверительный интервал.
Вы обратите внимание, что склонность понимать статистические параметры как обоснованные реальностью приводят к интересному следствию: исследователи склонны и не доверять и не придавать значения различиям, допустим в 10%, полученным при малых выборках, как ФОРМАЛЬНО недостоверным, но тем же самым значениям при больших выборках склонны приписывать огромное значения различиям в десятые доли процента (например, различия в доли телесмотрения, сколько копий сломанно и денег потрачено). Но существенность различий не меняется же от объема выборки, 10% в любом случае на два порядка больше десятых долей процента...
Еще в одной области с большим разнообразием признаков - в лингвистике - нормы ассоциативных экспериментов составляют 100 мужчин и 100 женщин, так как было показано, что при большем количестве респондентов новых ассоциаций выявлено не будет (то есть, появление новых ЕДИНИЧНЫХ значений возможно, но на показатели ассоциативной НОРМЫ - набор и доля устойчивых ассоциаций - это уже не влияет). Так что, как ни крути, для СОЦИОЛОГИЧЕСКОГО анализа, то есть ориентированного на выявление тех или иных массовых явлений, достаточно сравнительно малого числа респондентов (200-400).
То есть, вопрос точности измерения и сути получаемых результатов не очень сильно зависит от объема выборки (в общем случае мы можем исходить из того, что достоверны все результаты больше p=2,3/n) , а гораздо больше зависит от корректности формирования выборки и правильности используемых методов получения данных. |
|
<
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
17.02.2008 13:39 |  |
|
|
|
Постов: 2758
Дата регистрации: 31.08.2005 |
для: Developer© Ваша таблица только демонстрирует значимость правильного формирования выборки. Практическая проблема в том, что корректность формирования выборки оказывается важнее всяких там табличных значений. В наших задачах, когда нужно не шары из ящика выбирать, а формировать выборку из людей, ошибки формирования оказывают гораздо большее влияние на получаемые результаты, чем смещения, даваемые выборочным методом как таковым. Что такое 12 человек в выборке с признаком, который должен был быть выявлен только у 4? Плохая организация полевых работ, "поиск под фонарем, а не там, где потеряли".
Вот тот же лентяй Стьюдент, ну доказал он, что доля выявляемого пойла из партий пива существенно не меняется при выборочном методе по сравнению с плошным обследованием. Разница в том, что потребителю не важна ошибка в выявлении пойла, он заинтересован в абсолютном исключении пойла из поставок в магазины и бары.
В наших же задачах мы часто не знаем истинного значения изучаемого признака, из-за этого можем доверять получаемым значениям только исходя из репрезентативности известных параметров: пол, возраст, образование, распределение по уровню доходов и т.д. А тут получается интересная штука, что, если исключить ситуации подлога интервьеров по регистрации этих базовых параметров, то при квотных выборках в 60 человек и при репрезентативных по городу в 400 человек все необходимые параметры стабилизируются (на национальных выборках с 1200). Соответственно, и получаемые результаты по малым величинам тоже (том в смысле, что при увеличении выборки они будут только потихоньку снижатся, но НИКОГДА не будут выше полученных значений на этих выборках).
Нас же что волнует в вопросе выборочных исследований: сколько людей мы должны опросить, чтобы выявить все разнообразие признаков, и сколько, чтобы не ошибаться в их выраженности. Ответ на эти вопросы очень сильно зависит от того, что значит "разнообразие": признак, встречающийся у отдельных экземпляров нас интересует? А три ореха это куча? ТО есть это вопросы уже не самой статистики, а совсем другого. В принципе, общая склонность к использованию 95% вероятности позволяет предположить, что исследовательское сообщество склонно игнорировать признаки, которые имеют выраженность менее 5%. На самом деле, сто лет назад так оно и было; сейчас же готовы рассматривать любые малые группы и вообще маркетинговая мода декларирует склонность к атропологическим исследованиям, а в них как раз уникальность важнее "общности".
Что же касается ошибки в определении выраженности признака, то тут очень важным является для чего мы что-то измеряем. Маркетологи склонны игнорировать, что управленческие решения по своей природе статистически очень грубы, или "да" или "нет", нельзя быть "немножко беременным". Соответственно, они ориентированны не на точные значения, а на пороговые (ниже определенного - не работаем, выше определенного - работаем), причем субъективно интерпретируемые. И уж точно, не на сравнении 0,6% и 0,72%, пусть они и получены на выборке хоть в десятки тысяч человек, так как это другие параметры, формирующие эти значения, куда важнее и куда грубее по своей природе, чем что стандартная ошибка или доверительный интервал.
Вы обратите внимание, что склонность понимать статистические параметры как обоснованные реальностью приводят к интересному следствию: исследователи склонны и не доверять и не придавать значения различиям, допустим в 10%, полученным при малых выборках, как ФОРМАЛЬНО недостоверным, но тем же самым значениям при больших выборках склонны приписывать огромное значения различиям в десятые доли процента (например, различия в доли телесмотрения, сколько копий сломанно и денег потрачено). Но существенность различий не меняется же от объема выборки, 10% в любом случае на два порядка больше десятых долей процента...
Еще в одной области с большим разнообразием признаков - в лингвистике - нормы ассоциативных экспериментов составляют 100 мужчин и 100 женщин, так как было показано, что при большем количестве респондентов новых ассоциаций выявлено не будет (то есть, появление новых ЕДИНИЧНЫХ значений возможно, но на показатели ассоциативной НОРМЫ - набор и доля устойчивых ассоциаций - это уже не влияет). Так что, как ни крути, для СОЦИОЛОГИЧЕСКОГО анализа, то есть ориентированного на выявление тех или иных массовых явлений, достаточно сравнительно малого числа респондентов (200-400).
То есть, вопрос точности измерения и сути получаемых результатов не очень сильно зависит от объема выборки (в общем случае мы можем исходить из того, что достоверны все результаты больше p=2,3/n, по крайней мере, мы можем быть уверенны, что признаки не имеют выраженность больше полученной) , а гораздо больше зависит от корректности формирования выборки и правильности используемых методов получения данных. |
|
--------
http://www.dnp.ru |
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
    17.02.2008 13:41 17.02.2008 13:41 |  |
|
|
|
Постов: 8
Дата регистрации: 16.02.2008 |
Цитата, автор Михаил Дымшиц:
Так что, как ни крути, для СОЦИОЛОГИЧЕСКОГО анализа, то есть ориентированного на выявление тех или иных массовых явлений, достаточно сравнительно малого числа респондентов (200-400)....
|
В целом совершенно с Вами согласен, но в частности задача была поставлена Юрием для 1%.
Вот здесь, мои эксперименты и показывают что даже с точки зрения случайного отбора, 400 человек недостаточно.
12 вместо 4 при выборке 400 получается чисто случайно в 5% случаев (мой эксперимент). И фонарь здесь не причем - все квотировать невозможно.
То что организация полевых работ даст погрешность гораздо больше, здесь я с Вами абсолютно согласен, но хочется понять ситуацию и в теории и на практике
Пример: в случайной выборке 400 частота равна 0. Какая будет ошибка?
|
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 19:56 17.02.2008 19:56 |  |
|
|
|
Постов: 2128
Дата регистрации: 07.04.2005 |
Цитата, автор Developer:
….
Я провел эксперименты для а=1% при n=200, n=400, n=1200 картинака примерно одинаковая - смещение к 0.
|
Возможно у вас где-то вкралась ошибка при построении кривых. Если я правильно вас понял, вы привели 3 графика для:
а=1% при n=200, n=400, n=1200 соответственно. Так? И если ДА:
Тогда на ваших 3-х графиках максимумы должны находится по оси Х в точках:
na=200*1%=2; na=400*1%=4 и na=1200*1%=12 соответственно. А у вас такого смещения нет! Почему?
|
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 20:20 17.02.2008 20:20 |  |
|
|
|
Постов: 2758
Дата регистрации: 31.08.2005 |
Цитата, автор Developer:
Пример: в случайной выборке 400 частота равна 0. Какая будет ошибка?
|
стандартная ошибка 0% (и 100%)при n=400 0,0025063. |
|
--------
http://www.dnp.ru |
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
    17.02.2008 22:02 17.02.2008 22:02 |  |
|
|
|
Постов: 2128
Дата регистрации: 07.04.2005 |
Миша, со всем что вы пишите я в целом согласен.
В этих 2-х моих вопросах ответ должен быть точный!!! И когда авторитетные исследователи к примеру мне говорят:
1. Что выборка «200» достаточна для решения таких-то задач – я это принимаю к практическим действиям, при этом я всегда попытаюсь это хоть как-то обосновать. Собственно когда известна функция распределения (Бином) – эта задача решаема всегда.
См. рис. ниже. Лично для себя этот вопрос я считаю почти закрытым. И если эта тема кому нибудь помогла так и очень хорошо.
2.Увы пока мне никто не оппонировал о НЕ МОНОТОННОСТИ признака (кроме Игоря). Дело в том, что довольно часто в обсуждениях я слышу, что «что-то там» ведет себя горбато-образно (Игорь) или логнормально (Эдуард) и я по ходу жизни часто просто киваю… возможно не понимая что они имеют ввиду. Это меня начало мал-мало напрягать.
Я искренне не понимаю как связана не монотонность измеряемого признака в ГС и собственно измерения этого признака выборочным методом (случайная выборка).
(см. мой пример с расходами на моб. связь - я там почти на каждой точке указал что она распределена нормально…. )
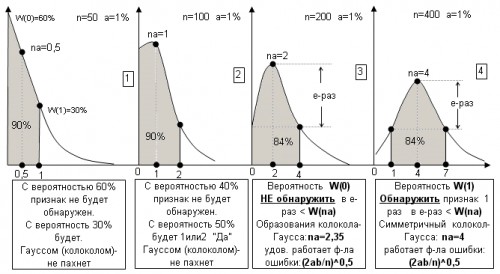
Во всех моих постах ваше принят постулат – максимальная вероятность получения ответа «Да» равна доле признака (а). Этот постулат нарушается в биномиальном распределении (см 1 и 2 графики ниже) – лишь в условиях малой выборки исследуемого признака. Другими словами, вероятность не обнаружить этот признак является максимальной …
|
|
 | | Ошибка 5.gif |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 23:02 17.02.2008 23:02 |  |
|
|
|
Постов: 2128
Дата регистрации: 07.04.2005 |
| А чей пост Гостя от 17.02.2008 11:06 ??? кстати ОЧень содержательный! |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   17.02.2008 23:20 17.02.2008 23:20 |  |
|
|
|
Постов: 8
Дата регистрации: 16.02.2008 |
Цитата, автор Юрий Рязанов:
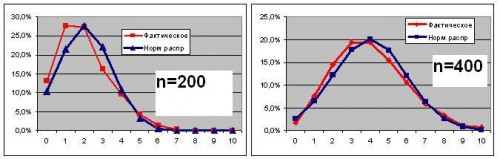
Тогда на ваших 3-х графиках максимумы должны находится по оси Х в точках:
na=200*1%=2; na=400*1%=4 и na=1200*1%=12 соответственно. А у вас такого смещения нет! Почему?
|
Верно заметили - ошибка (хотел получить в %, но там действительно частоты)
и теперь все соответсвует Вашим предыдущим расчетам.
А я то думаю, почему сначала у меня результаты с Вашими сошлись, а потом расходятся...
Соответственно таблица в последней строке тоже некооректна и расхождений нет.
|
|
 | | а=1.JPG |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   18.02.2008 00:42 18.02.2008 00:42 |  |
|
|
|
Постов: 2758
Дата регистрации: 31.08.2005 |
Цитата, автор Юрий Рязанов:
А чей пост Гостя от 17.02.2008 11:06 ??? кстати ОЧень содержательный! |
Юра, это мой |
|
--------
http://www.dnp.ru |
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
    18.02.2008 08:48 18.02.2008 08:48 |  |
|
|
|
Постов: 2758
Дата регистрации: 31.08.2005 |
Цитата, автор Юрий Рязанов:
Я искренне не понимаю как связана не монотонность измеряемого признака в ГС и собственно измерения этого признака выборочным методом (случайная выборка).
|
Юра, "горбато-образность" часто является следствием размерности шкалы: выберешь другой шаг шкалы, разобъешь на другое число диапазонов, и "дополнительные горбы" могут исчезнуть  . "На самом деле", на исполуемость выборочного метода это никак не влияет. Даже если там и есть "выбросы", то если они значимые, то они при достаточно большой выборке будут выявленны, если они составляют мизерную долю, так и фиг с ними. Тем более, не попадает под эту "проблему" логнормальные или другого типа распределения (Ципфа и т.д.), так как они все являются по своей сути вариантами нормального распределения. . "На самом деле", на исполуемость выборочного метода это никак не влияет. Даже если там и есть "выбросы", то если они значимые, то они при достаточно большой выборке будут выявленны, если они составляют мизерную долю, так и фиг с ними. Тем более, не попадает под эту "проблему" логнормальные или другого типа распределения (Ципфа и т.д.), так как они все являются по своей сути вариантами нормального распределения.
Настоящая проблема исследователей как раз в том, что "хвост" распределения ну никак не попадает под "нормальность". Как в примере по сотовой связи - большие значения в самом конце не апроксимируются к Х, а хотят рвануть вверх. Проблема усугбляется еще тем, что при более подробном исследовании "хвоста" это желание становится весьма очевидным. И, конечно, ни под какие "нормальные" виды распределения это уже не попадает... Проблема то в том, что мы склонны рассматривать рынки как в том или ином смысле единые и ожидаем от них "нормальное" распределенные, а "на самом деле" в дорогих хвостах совсем другая жизнь, это другая группа. Это просто особенность такого объекта изучения, как общество, "нормальности", чтобы под этим не понимали, от него ждать не стоит   |
|
--------
http://www.dnp.ru |
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
    18.02.2008 09:06 18.02.2008 09:06 |  |
|
|
|
Постов: 2128
Дата регистрации: 07.04.2005 |
Цитата, автор Михаил Дымшиц :
.....
Если нет перекоса при формировании выборки, то малые доли НИКОГДА не будут расти при увеличении выборки .... |
Вот это ваше утверждение на самом деле далеко не очевидное. Но по сути ОЧень правильное. И точно, что эта тема отдельного разговора!
Если очень кратко, то по сути этот тезис можно трактовать так:
-если процесс стационарный во времени то увеличение выборки никогда не даст увеличение доли. А если процесс не стационарный так его и не надо брать в расчет в следствии его высокой не определенности……
Цитата, автор Михаил Дымшиц :
….Но это общая уверенность в типичности "нормального распределения" является последствием травм, полученных в системе образования.
|
На мой взгляд должно выполнятся простое требование, чтобы распределение:
1) Было приемлемой формы (желательно c симметричным колоколом ;) )
2) Позволяло легко проводить вычисления(чего я здесь и добиваюсь  ) )
Собственно, я этому и следую с самого начала, когда требую что бы вероятность не обнаружить признак была в e-раз! меньше максимальной (по сути это кусок/крючёк колокола). Проще говоря, я ставлю условие существования колокола (пусть и не особо симметричного). У Гаусса это требование соответствует 84% вероятности (84% - это площадь колокола)….
А вот уже для принятой в индустрии вероятности 95% (площадь колокола), условие получается очень близкое в e^e раз! это ~в 15 раз.
Цитата, автор Михаил Дымшиц :
………..Вообще, когда спорят о точности измерения малых величин как-то забывают, что в этой ситуации можно обсуждать точность величин (1-p) и тогда спор теряет смысл, так как относительная ошибка становится на порядок меньше.
|
Миша, распределение симметрично относительно доли, так что без разницы какую анализировать долю a или ее отсутствие b=(1-a) (простая замена переменных и вид тот же самый).
И тем не менее хотелось бы поставить точку в этом вопросе. Поэтому я решил в приведенных ниже уравнениях уже не пренебрегая членом (1-a). И в том числе сделать оценку для принятой индустрией вероятностью 95%.
Не составляет труда численно решить уравнения:
Wmax/W(0)=e (20) - это для колокола площадью ~84%
Wmax/W(0)=e^e (21) - это для колокола площадью ~95%
и соответственно найти зависимость доли a от объема выборки n. Запишем эти уравнения:
(1-a)^n[2Пи n a(1-a)]^0.5=e^-1 – это для вероятности 84%
(1-a)^n[2Пи n a(1-a)]^0.5=e^-e – это для вероятности 95%
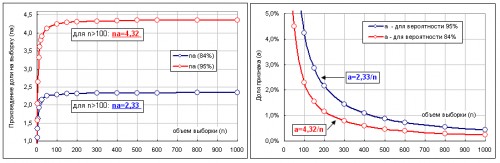
С ОЧень хорошей точностью, можно утверждать что произведение доли на объем выборки – const См. графики полученные путем численного решения уравнений 20 и 21.
na=2.3 - для (84%) и n>100; тогда ф-ла ошибки D=+-(2ab/n)^0.5
na=4.3 - для (95%) и n>100; тогда ф-ла ошибки D=+-1.96(ab/n)^0.5
Дополнительная информация к графикам:
Вероятность не обнаружить признак:
1) для вероятности 84%: W(0)=10% для выборки n>100
2) для вероятности 95%: W(0)=1.5% для выборки n>100
P.S. Миша, я согласен с вами что для малых долей - с ошибками конечно все ОЧень мутно… Это есть следствие разрыва статистик. Бином кончился, а Пуассон еще не начался….. и никогда не начнется, поскольку социальные признаки не всегда стационарны!!! И тем не менее пусть и несколько формально, но говорить об ошибках малых признаков когда выполнено условие n>2.3/a (и тем паче n>4.3/а) можно, поскольку хоть плохонький/кривой но колокольчик(скорее даже крючёк) всеж таки есть ;) . Увы, а другого распределения (отличного от бинома) описывающего малые признаки у нас просто нет.
|
|
 | | Ошибка 6.gif |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   18.02.2008 22:50 18.02.2008 22:50 |  |
|
|
|
Постов: 2128
Дата регистрации: 07.04.2005 |
Цитата, автор Михаил Дымшиц:
"На самом деле", на исполуемость выборочного метода это никак не влияет. Даже если там и есть "выбросы", то если они значимые, то они при достаточно большой выборке будут выявленны, если они составляют мизерную долю, так и фиг с ними. |
По этому вопросу (про не монотоность признака) у нас с вами полное согласие. И это радует. 
|
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   18.02.2008 23:07 18.02.2008 23:07 |  |
|
|
|
Постов: 2114
Дата регистрации: 01.09.2005 |
для: Developer©
Добрый вечер.
Спасибо понятно. |
|
 |
0 |
 |
0 |
| Комментарий понравился? |
 |
0 |
 |
0 |
   18.02.2008 23:36 18.02.2008 23:36 |  |
|
|
|
 | Только зарегистрированные пользователи могут оставлять сообщения в этом форуме |
|
 |
 |
 |
|
© "ООО Состав.ру" 1998-2025
тел/факс: +7 495 225 1331 адрес: 109004, Москва, Пестовский пер., д. 16, стр. 2
При использовании материалов портала ссылка на Sostav.ru обязательна!
Администрация Sostav.ru просит Вас сообщать о всех замеченных технических неполадках на E-mail
|
|
|
|
















 ).
).






 . "На самом деле", на исполуемость выборочного метода это никак не влияет. Даже если там и есть "выбросы", то если они значимые, то они при достаточно большой выборке будут выявленны, если они составляют мизерную долю, так и фиг с ними. Тем более, не попадает под эту "проблему" логнормальные или другого типа распределения (Ципфа и т.д.), так как они все являются по своей сути вариантами нормального распределения.
. "На самом деле", на исполуемость выборочного метода это никак не влияет. Даже если там и есть "выбросы", то если они значимые, то они при достаточно большой выборке будут выявленны, если они составляют мизерную долю, так и фиг с ними. Тем более, не попадает под эту "проблему" логнормальные или другого типа распределения (Ципфа и т.д.), так как они все являются по своей сути вариантами нормального распределения.













